CBSE Class 10 Maths - MCQ and Online Tests - Unit 2 - Polynomials

CBSE Class 10 Maths – MCQ and Online Tests – Unit 2 – Polynomials

Every year CBSE conducts board exams for 10th standard. These exams are very competitive to all the students. So our website provides online tests for all the 10th subjects. These tests are also very effective and useful for those who preparing for competitive exams like NEET, JEE, CA etc. It can boost their preparation level and confidence level by attempting these chapter wise online tests.

These online tests are based on latest CBSE Class 10 syllabus. While attempting these our students can identify the weak lessons and continuously practice those lessons for attaining high marks. It also helps to revise the NCERT textbooks thoroughly.

 

CBSE Class 10 Maths – MCQ and Online Tests – Unit 2 – Polynomials

Question 1.
The maximum number of zeroes that a polynomial of degree 4 can have is
(a) One
(b) Two
(c) Three
(d) Four

Answer

Answer: (d) Four

---

Question 2.
The graph of the polynomial p(x) = 3x – 2 is a straight line which intersects the x-axis at exactly one point namely
(a) (\(\frac{-2}{3}\), 0)
(b) (0, \(\frac{-2}{3}\))
(c) (\(\frac{2}{3}\), 0)
(d) \(\frac{2}{3}\), \(\frac{-2}{3}\)

Answer

Answer: (c) (\(\frac{2}{3}\), 0)

---

Question 3.
In fig. given below, the number of zeroes of the polynomial f(x) is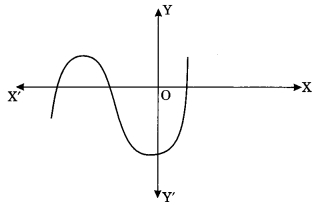

(a) 1
(b) 2
(c) 3
(d) None

Answer

Answer: (c) 3

---

Question 4.
The graph of the polynomial ax² + bx + c is an upward parabola if
(a) a > 0
(b) a < 0
(b) a = 0
(d) None

Answer

Answer: (a) a > 0

---

Question 5.
The graph of the polynomial ax² + bx + c is a downward parabola if
(a) a > 0
(b) a < 0
(c) a = 0
(d) a = 1

Answer

Answer: (b) a < 0

---

Question 6.
A polynomial of degree 3 is called
(a) a linear polynomial
(b) a quadratic polynomial
(c) a cubic polynomial
(d) a biquadratic polynomial

Answer

Answer: (c) a cubic polynomial

---

Question 7.
If α, β are the zeroes of the polynomial x² – 16, then αβ(α + β) is
(a) 0
(b) 4
(c) -4
(d) 16

Answer

Answer: (a) 0

---

Question 8.
If α and \(\frac{1}{α}\) are the zeroes of the polynomial ax² + bx + c, then value of c is
(a) 0
(b) a
(c) -a
(d) 1

Answer

Answer: (b) a

---

Question 9.
Zeroes of the polynomial x² – 11 are
(a) ±\(\sqrt{17}\)
(b) ±\(\sqrt{3}\)
(c) 0
(d) None

Answer

Answer: (a) ±\(\sqrt{17}\)

---

Question 10.
If α, β, γ are the zeroes of the cubic polynomial ax³ + bx² + cx + d then α + β + γ is equal
(a) \(\frac{-b}{a}\)
(b) \(\frac{b}{a}\)
(c) \(\frac{c}{a}\)
(d) \(\frac{d}{a}\)

Answer

Answer: (a) \(\frac{-b}{a}\)

---

Question 11.
If α, β, γ are the zeroes of the cubic polynomial ax³ + bx² + cx + d then αβ + βγ + αγ is equal to
(a) \(\frac{-b}{a}\)
(b) \(\frac{b}{a}\)
(c) \(\frac{c}{a}\)
(d) \(\frac{d}{a}\)

Answer

Answer: (c) \(\frac{c}{a}\)

---

Question 12.
If the zeroes of the polynomial x³ – 3x² + x – 1 are \(\frac{s}{t}\), s and st then value of s is
(a) 1
(b) -1
(c) 2
(d) -3

Answer

Answer: (a) 1

---

Question 13.
If the sum of the zeroes of the polynomial f(x) = 2x³ – 3kx² + 4x – 5 is 6, then the value of k is
(a) 2
(b) 4
(c) -2
(d) -4

Answer

Answer: (b) 4

---

Question 14.
If a polynomial of degree 4 is divided by quadratic polynomial, the degree of the remainder is
(a) ≤ 1
(b) ≥ 1
(c) 2
(d) 4

Answer

Answer: (a) ≤ 1

---

Question 15.
If a – b, a and a + b are zeroes of the polynomial fix) = 2x³ – 6x² + 5x – 7, then value of a is
(a) 1
(b) 2
(c) -5
(d) 7

Answer

Answer: (a) 1

---

Question 16.
Dividend is equal to
(a) divisor × quotient + remainder
(b) divisior × quotient
(c) divisior × quotient – remainder
(d) divisor × quotient × remainder

Answer

Answer: (a) divisor × quotient + remainder

---

Question 17.
A quadratic polynomial whose sum of the zeroes is 2 and product is 1 is given by
(a) x² – 2x + 1
(b) x² + 2x + 1
(c) x² + 2x – 1
(d) x² – 2x – 1

Answer

Answer: (a) x² – 2x + 1

---

Question 18.
If one of the zeroes of a quadratic polynomial ax² + bx + c is 0, then the other zero is
(a) \(\frac{-b}{a}\)
(b) 0
(c) \(\frac{b}{a}\)
(d) \(\frac{-c}{a}\)

Answer

Answer: (a) \(\frac{-b}{a}\)

---

Question 19.
The sum and the product of the zeroes of polynomial 6x² – 5 respectively are
(a) 0, \(\frac{-6}{5}\)
(b) 0, \(\frac{6}{5}\)
(c) 0, \(\frac{5}{6}\)
(d) 0, \(\frac{-5}{6}\)

Answer

Answer: (d) 0, \(\frac{-5}{6}\)

---

Question 20.
What should be subtracted from x³ – 2x² + 4x + 1 to get 1?
(a) x³ – 2x² + 4x
(b) x³ – 2x² + 4 + 1
(c) -1
(d) 1

Answer

Answer: (a) x³ – 2x² + 4x

---