CBSE Class 12 Maths – MCQ and Online Tests – Unit 12 – Linear Programming
Every year CBSE conducts board exams for 12th standard. These exams are very competitive to all the students. So our website provides online tests for all the 12th subjects. These tests are also very effective and useful for those who preparing for competitive exams like NEET, JEE, CA etc. It can boost their preparation level and confidence level by attempting these chapter wise online tests.
These online tests are based on latest CBSE Class 12 syllabus. While attempting these our students can identify the weak lessons and continuously practice those lessons for attaining high marks. It also helps to revise the NCERT textbooks thoroughly.
CBSE Class 12 Maths – MCQ and Online Tests – Unit 12 – Linear Programming
Question 1.
The maximum value of Z = 4x + 2y subject to the constraints 2x + 3y ≤ 18, x + y ≥ 10, x, y ≤ 0 is
(a) 36
(b) 40
(c) 30
(d) None of these
Answer
Answer: (d) None of these
Question 2.
In equation 3x – y ≥ 3 and 4x – 4y > 4
(a) Have solution for positive x and y
(b) Have no solution for positive x and y
(c) Have solution for all x
(d) Have solution for all y
Answer
Answer: (a) Have solution for positive x and y
Question 3.
Maximize Z = 3x + 5y, subject to x + 4y ≤ 24, 3x + y ≤ 21, x + y ≤ 9, x ≥ 0, y ≥ 0
(a) 20 at (1, 0)
(b) 30 at (0, 6)
(c) 37 at (4, 5)
(d) 33 at (6, 3)
Answer
Answer: (c) 37 at (4, 5)
Question 4.
The maximum value of Z = 3x + 4y subjected to contraints x + y ≤ 40, x + 2y ≤ 60, x ≥ 0 and y ≥ 0 is
(a) 120
(b) 140
(c) 100
(d) 160
Answer
Answer: (b) 140
Question 5.
Maximize Z = 7x + 11y, subject to 3x + 5y ≤ 26, 5x + 3y ≤ 30, x ≥ 0, y ≥ 0
(a) 59 at (\(\frac{9}{2}\), \(\frac{5}{2}\))
(b) 42 at (6, 0)
(c) 49 at (7, 0)
(d) 57.2 at (0, 5.2)
Answer
Answer: (a) 59 at (\(\frac{9}{2}\), \(\frac{5}{2}\))
Question 6.
Maximize Z = 11 x + 8y subject to x ≤ 4, y ≤ 6, x + y ≤ 6, x ≥ 0, y ≥ 0.
(a) 44 at (4, 2)
(b) 60 at (4, 2)
(c) 62 at (4, 0)
(d) 48 at (4, 2)
Answer
Answer: (b) 60 at (4, 2)
Question 7.
Feasible region in the set of points which satisfy
(a) The objective functions
(b) Some the given constraints
(c) All of the given constraints
(d) None of these
Answer
Answer: (c) All of the given constraints
Question 8.
A set of values of decision variables which satisfies the linear constraints and nn-negativity conditions of a L.P.P. is called its
(a) Unbounded solution
(b) Optimum solution
(c) Feasible solution
(d) None of these
Answer
Answer: (c) Feasible solution
Question 9.
Maximize Z = 4x + 6y, subject to 3x + 2y ≤ 12, x + y ≥ 4, x, y ≥ 0
(a) 16 at (4, 0)
(b) 24 at (0, 4)
(c) 24 at (6, 0)
(d) 36 at (0, 6)
Answer
Answer: (d) 36 at (0, 6)
Question 10.
Maximize Z = 6x + 4y, subject to x ≤ 2, x + y ≤ 3, -2x + y ≤ 1, x ≥ 0, y ≥ 0
(a) 12 at (2, 0)
(b) \(\frac{140}{3}\) at (\(\frac{2}{3}\), \(\frac{1}{3}\))
(c) 16 at (2, 1)
(d) 4 at (0, 1)
Answer
Answer: (c) 16 at (2, 1)
Question 11.
Maximize Z = 10 x1 + 25 x2, subject to 0 ≤ x1 ≤ 3, 0 ≤ x2 ≤ 3, x1 + x2 ≤ 5
(a) 80 at (3, 2)
(b) 75 at (0, 3)
(c) 30 at (3, 0)
(d) 95 at (2, 3)
Answer
Answer: (d) 95 at (2, 3)
Question 12.
Z = 20x1 + 202, subject to x1 ≥ 0, x2 ≥ 0, x1 + 2x2 ≥ 8, 3x1 + 2x2 ≥ 15, 5x1 + 2x2 ≥ 20. The minimum value of Z occurs at
(a) (8, 0)
(b) (\(\frac{5}{2}\), \(\frac{15}{4}\))
(c) (\(\frac{7}{2}\), \(\frac{9}{4}\))
(d) (0, 10)
Answer
Answer: (c) (\(\frac{7}{2}\), \(\frac{9}{4}\))
Question 13.
Refer to Question 18 (Maximum value of Z+ Minimum value of Z) is equal to
(a) 13
(b) 1
(c) -13
(d) -17
Answer
Answer: (d) -17
Question 14.
Z = 6x + 21 y, subject to x + 2y ≥ 3, x + 4y ≥ 4, 3x + y ≥ 3, x ≥ 0, y ≥ 0. The minimum value of Z occurs at
(a) (4, 0)
(b) (28, 8)
(c) (2, \(\frac{7}{2}\))
(d) (0, 3)
Answer
Answer: (c) (2, \(\frac{7}{2}\))
Question 15.
Of all the points of the feasible region for maximum or minimum of objective function the points
(a) Inside the feasible region
(b) At the boundary line of the feasible region
(c) Vertex point of the boundary of the feasible region
(d) None of these
Answer
Answer: (c) Vertex point of the boundary of the feasible region
Question 16.
The corner point of the feasible region determined by the system of linear constraints are (0, 0), (0, 40), (20, 40), (60, 20), (60, 0). The objective function is Z = 4x + 3y.
Compare the quantity in Column A and Column B
| Column A | Column B |
| Maximum of Z | 325 |
(a) The quantity in column A is greater
(b) The quantity in column B is greater
(c) The two quantities are equal
(d) The relationship cannot be determined On the basis of the information supplied
Answer
Answer: (b) The quantity in column B is greater
Question 17.
The maximum value of the object function Z = 5x + 10 y subject to the constraints x + 2y ≤ 120, x + y ≥ 60, x – 2y ≥ 0, x ≥ 0, y ≥ 0 is
(a) 300
(b) 600
(c) 400
(d) 800
Answer
Answer: (b) 600
Question 18.
The feasible region for a LPP is shown shaded in the figure. Let Z = 3x – 4y be the objective function. Minimum of Z occurs at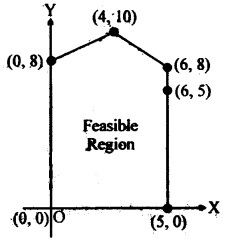
(a) (0, 0)
(b) (0, 8)
(c) (5, 0)
(d) (4, 10)
Answer
Answer: (b) (0, 8)
Question 19.
Objective function of a linear programming problem is
(a) a constraint
(b) function to be obtimized
(c) A relation between the variables
(d) None of these
Answer
Answer: (b) function to be obtimized
Question 20.
Refer to Question 18 maximum of Z occurs at
(a) (5, 0)
(b) (6, 5)
(c) (6, 8)
(d) (4, 10)
Answer
Answer: (a) (5, 0)














0 Comments:
Post a Comment