CBSE Class 12 Maths – MCQ and Online Tests – Unit 5 – Continuity and Differentiability
Every year CBSE conducts board exams for 12th standard. These exams are very competitive to all the students. So our website provides online tests for all the 12th subjects. These tests are also very effective and useful for those who preparing for competitive exams like NEET, JEE, CA etc. It can boost their preparation level and confidence level by attempting these chapter wise online tests.
These online tests are based on latest CBSE Class 12 syllabus. While attempting these our students can identify the weak lessons and continuously practice those lessons for attaining high marks. It also helps to revise the NCERT textbooks thoroughly.
CBSE Class 12 Maths – MCQ and Online Tests – Unit 5 – Continuity and Differentiability
Question 1.
If f(x) =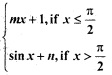
is continuous at x = \(\frac{π}{2}\), then
(a) m = 1, n = 0
(b) m = \(\frac{nπ}{2}\) + 1
(c) n = \(\frac{mπ}{2}\)
(d) m = n = \(\frac{π}{2}\)
Answer
Answer: (c) n = \(\frac{mπ}{2}\)
Question 2.
Let f(x) = |sin x| Then
(a) f is everywhere differentiable
(b) f is everywhere continuous but not differentiable at x = nπ, n ∈ Z
(c) f is everywhere continuous but no differentiable at x = (2n + 1) \(\frac{π}{2}\) n ∈ Z
(d) None of these
Answer
Answer: (b) f is everywhere continuous but not differentiable at x = nπ, n ∈ Z
Question 3.
If y = \(\sqrt{sin x+y}\) then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{cosx}{2y-1}\)
(b) \(\frac{cosx}{1-2y}\)
(c) \(\frac{sinx}{1-xy}\)
(d) \(\frac{sinx}{2y-1}\)
Answer
Answer: (a) \(\frac{cosx}{2y-1}\)
Question 4.
If sec (\(\frac{x-y}{x+y}\)) = a then \(\frac{dy}{dx}\) is
(a) –\(\frac{y}{x}\)
(b) \(\frac{x}{y}\)
(c) –\(\frac{x}{y}\)
(d) \(\frac{y}{x}\)
Answer
Answer: (d) \(\frac{y}{x}\)
Question 5.
The derivative of cos-1 (2x² – 1) w.r.t cos-1 x is
(a) 2
(b) \(\frac{-1}{2\sqrt{1-x^2}}\)
(c) \(\frac{2}{x}\)
(d) 1 – x²
Answer
Answer: (a) 2
Question 6.
If x = t², y = t³, then \(\frac{d^2y}{dx^2}\)
(a) \(\frac{3}{2}\)
(b) \(\frac{3}{4t}\)
(c) \(\frac{3}{2t}\)
(d) \(\frac{3}{4t}\)
Answer
Answer: (b) \(\frac{3}{4t}\)
Question 7.
If y = log(\(\frac{1-x^2}{1+x^2}\)), then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{4x^3}{1-x^4}\)
(b) \(\frac{-4x}{1-x^4}\)
(c) \(\frac{1}{4-x^4}\)
(d) \(\frac{-4x^3}{1-x^4}\)
Answer
Answer: (b) \(\frac{-4x}{1-x^4}\)
Question 8.
The value of c in Rolle’s theorem for the function f(x) = x³ – 3x in the interval [o, √3] is
(a) 1
(b) -1
(c) \(\frac{3}{2}\)
(d) \(\frac{1}{3}\)
Answer
Answer: (a) 1
Question 9.
If f (x) = 2x and g (x) = \(\frac{x^2}{2}\) + 1, then’which of the following can be a discontinuous function
(a) f(x) + g(x)
(b) f(x) – g(x)
(c) f(x).g(x)
(d) \(\frac{g(x)}{f(x)}\)
Answer
Answer: (d) \(\frac{g(x)}{f(x)}\)
Question 10.
For the function f(x) = x + \(\frac{1}{x}\), x ∈ [1, 3] the value of c for mean value theorem is
(a) 1
(b) √3
(c) 2
(d) None of these
Answer
Answer: (b) √3
Question 11.
Let function f (x) =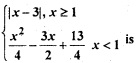 
(a) continuous at x = 1
(b) differentiable at x = 1
(c) continuous at x = -3
(d) All of these
Answer
Answer: (d) All of these
Question 12.
If x sin (a + y) = sin y, then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{sin^2(a+y)}{sin a}\)
(b) \(\frac{sin a}{sin^2(a+y)}\)
(c) \(\frac{sin(a+y)}{sin a}\)
(d) \(\frac{sin a}{sin(a+y)}\)
Answer
Answer: (a) \(\frac{sin^2(a+y)}{sin a}\)
Question 13.
The set of points where the function f given by f (x) =| 2x – 1| sin x is differentiable is
(a) R
(b) R = {\(\frac{1}{2}\)}
(c) (0, ∞)
(d) None of these
Answer
Answer: (b) R = {\(\frac{1}{2}\)}
Question 14.
If sec(\(\frac{x^2-2x}{x^2+1}\)) – y then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{y*2}{x^2}\)
(b) \(\frac{2y\sqrt{y^2-1}(x^2+x-1)}{(x^2+1)^2}\)
(c) \(\frac{(x^2+x-1)}{y\sqrt{y^2-1}}\)
(d) \(\frac{x^2-y^2}{x^2+y^2}\)
Answer
Answer: (b) \(\frac{2y\sqrt{y^2-1}(x^2+x-1)}{(x^2+1)^2}\)
Question 15.
If y = tan-1(\(\frac{sinx+cosx}{cox-sinx}\)) then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{1}{2}\)
(b) \(\frac{π}{4}\)
(c) 0
(d) 1
Answer
Answer: (d) 1
Question 16.
The function f(x) = cot x is discontinuous on the set
(a) {x = nπ, n ∈ Z}
(b) {x = 2nπ, n ∈ Z}
(c) {x = (2n + 1) \(\frac{π}{2}\) n ∈ Z}
(d) {x – \(\frac{nπ}{2}\) n ∈ Z}
Answer
Answer: (a) {x = nπ, n ∈ Z}
Question 17.
Differential coefficient of \(\sqrt{sec√x}\) is
(a) \(\frac{1}{4√x}\) = sec √x sin √x
(b) \(\frac{1}{4√x}\) = (sec√x)3/2 sin√x
(c) \(\frac{1}{2}\) √x sec√x sin √x.
(d) \(\frac{1}{2}\)√x (sec√x)3/2 sin√x
Answer
Answer: (b) \(\frac{1}{4√x}\) = (sec√x)3/2 sin√x
Question 18.
If f(x) = \(\frac{\sqrt{4+x}-2}{x}\) x ≠ 0 be continuous at x = 0, then f(o) =
(a) \(\frac{1}{2}\)
(b) \(\frac{1}{4}\)
(c) 2
(d) \(\frac{3}{2}\)
Answer
Answer: (b) \(\frac{1}{4}\)
Question 19.
let f(2) = 4 then f”(2) = 4 then \(_{x→2}^{lim}\) \(\frac{xf(2)-2f(x)}{x-2}\) is given by
(a) 2
(b) -2
(c) -4
(d) 3
Answer
Answer: (c) -4
Question 20.
The function f(x) = \(\frac{4-x^2}{4x-x^3}\) is
(a) discontinuous at only one point at x = 0
(b) discontinuous at exactly two points
(c) discontinuous at exactly three points
(d) None of these
Answer
Answer: (a) discontinuous at only one point at x = 0
Question 21.
It is given that f'(a) exists, then \(_{x→2}^{lim}\) [/latex] \(\frac{xf(a)-af(x)}{(x-a)}\) is equal to
(a) f(a) – af'(a)
(b) f'(a)
(c) -f’(a)
(d) f (a) + af'(a)
Answer
Answer: (a) f(a) – af'(a)
Question 22.
If y = ax² + b, then \(\frac{dy}{dx}\) at x = 2 is equal to ax
(a) 4a
(b) 3a
(c) 2a
(d) None of these
Answer
Answer: (a) 4a
Question 23.
If x \(\sqrt{1+y}+y\sqrt{1+x}\) = 0, then \(\frac{dy}{dx}\) =
(a) \(\frac{x+1}{x}\)
(b) \(\frac{1}{1+x}\)
(c) \(\frac{-1}{(1+x)^2}\)
(d) \(\frac{x}{1+x}\)
Answer
Answer: (c) \(\frac{-1}{(1+x)^2}\)
Question 24.
Let f be defined on [-5, 5] as
f(x) = {\(_{-x, if x is irrational}^{x, if x is rational}\) Then f(x) is
(a) continuous at every x except x = 0
(b) discontinuous at everyx except x = 0
(c) continuous everywhere
(d) discontinuous everywhere
Answer
Answer: (b) discontinuous at everyx except x = 0
Question 25.
If y = x tan y, then \(\frac{dy}{dx}\) =
(a) \(\frac{tan x}{x-x^2-y^2}\)
(b) \(\frac{y}{x-x^2-y^2}\)
(c) \(\frac{tan y}{y-x}\)
(d) \(\frac{tan x}{x-y^2}\)
Answer
Answer: (b) \(\frac{y}{x-x^2-y^2}\)
Question 26.
If f(x) = \(\sqrt{25-x^2}\), then \(_{x→2}^{lim}\)\(\frac{f(x)-f(1)}{x-1}\) is equal to
(a) \(\frac{1}{24}\)
(b) \(\frac{1}{5}\)
(c) –\(\sqrt{24}\)
(d) \(\frac{1}{\sqrt{24}}\)
Answer
Answer: (d) \(\frac{1}{\sqrt{24}}\)
Question 27.
If y = (1 + x) (1 + x²) (1 + x4) …….. (1 + x2n), then the value of \(\frac{dy}{dx}\) at x = 0 is
(a) 0
(b) -1
(c) 1
(d) None of these
Answer
Answer: (c) 1
Question 28.
If f(x) = \(\frac{5x}{(1-x)^{2/3}}\) + cos² (2x + 1), then f'(0) =
(a) 5 + 2 sin 2
(b) 5 + 2 cos 2
(c) 5 – 2 sin 2
(d) 5 – 2 cos 2
Answer
Answer: (c) 5 – 2 sin 2
Question 29.
If f(x) = \(\sqrt{1+cos^2(x^2)}\), then the value of f’ (\(\frac{√π}{2}\)) is
(a) \(\frac{√π}{6}\)
(b) –\(\frac{√π}{6}\)
(c) \(\frac{1}{√6}\)
(d) \(\frac{π}{√6}\)
Answer
Answer: (b) –\(\frac{√π}{6}\)
Question 30.
If xmyn = (x + y)m+n, then \(\frac{dy}{dx}\) is equal to
(a) \(\frac{x+y}{xy}\)
(b) xy
(c) \(\frac{x}{y}\)
(d) \(\frac{y}{x}\)
Answer
Answer: (d) \(\frac{y}{x}\)
Question 31.
If \(\sqrt{(x+y)}\) + \(\sqrt{(y-x)}\) = a, then \(\frac{dy}{dx}\)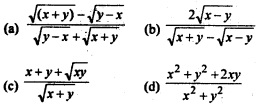
Answer
Answer: (a) \(\frac{\sqrt{(x+y)}-\sqrt{(y-x)}}{\sqrt{y-x}+\sqrt{x+y}}\)
Question 32.
The function f(x) = e|x| is
(a) continuous everywhere but not differentiable at x = 0
(b) continuous and differentiable everywhere
(c) not continuous at x = 0
(d) None of these
Answer
Answer: (a) continuous everywhere but not differentiable at x = 0
Question 33.
If f(x) = x² sin\(\frac{1}{x}\), where x ≠ 0, then the value of the function f(x) at x = 0, so that the function is continuous at x = 0 is
(a) 0
(b) -1
(c) 1
(d) None of these
Answer
Answer: (a) 0
Question 34.
Let f(x)={\(_{1-cos x, for x ≤ 0}^{sin x, for x > 0}\) and g (x) = ex. Then the value of (g o f)’ (0) is
(a) 1
(b) -1
(c) 0
(d) None of these
Answer
Answer: (c) 0
Question 35.
If ax² + 2hxy + by² = 1, then \(\frac{dy}{dx}\)equals
(a) \(\frac{hx+by}{ax+by}\)
(b) \(\frac{ax+by}{hx+by}\)
(c) \(\frac{ax+hy}{hx+hy}\)
(d) \(\frac{-(ax+hy)}{hx+by}\)
Answer
Answer: (d) \(\frac{-(ax+hy)}{hx+by}\)
0 Comments:
Post a Comment