CBSE Class 12 Maths - MCQ and Online Tests - Unit 1 - Relations and Functions

CBSE Class 12 Maths – MCQ and Online Tests – Unit 1 – Relations and Functions

Every year CBSE conducts board exams for 12th standard. These exams are very competitive to all the students. So our website provides online tests for all the 12th subjects. These tests are also very effective and useful for those who preparing for competitive exams like NEET, JEE, CA etc. It can boost their preparation level and confidence level by attempting these chapter wise online tests.

These online tests are based on latest CBSE Class 12 syllabus. While attempting these our students can identify the weak lessons and continuously practice those lessons for attaining high marks. It also helps to revise the NCERT textbooks thoroughly.

 

CBSE Class 12 Maths – MCQ and Online Tests – Unit 1 – Relations and Functions

Question 1.
If A, B and C are three sets such that A ∩ B = A ∩ C and A ∪ B = A ∪ C. then
(a) A = B
(b) A = C
(c) B = C
(d) A ∩ B = d

Answer

Answer: (c) B = C

---

Question 2.
Let A = {1, 2}, how many binary operations can be defined on this set?
(a) 8
(b) 10
(c) 16
(d) 20

Answer

Answer: (c) 16

---

Question 3.
If f: R → R defined by f(x) = 2x + 3 then f^-1(x) =
(a) 2x – 3
(b) \(\frac{x-3}{2}\)
(c) \(\frac{x+3}{2}\)
(d) None of these

Answer

Answer: (b) \(\frac{x-3}{2}\)

---

Question 4.
If an operation is defined by a* b = a² + b², then (1 * 2) * 6 is
(a) 12
(b) 28
(c) 61
(d) None of these

Answer

Answer: (c) 61

---

Question 5.
If A = (1, 2, 3}, B = {6, 7, 8} is a function such that f(x) = x + 5 then what type of a function is f?
(a) Many-one onto
(b) Constant function
(c) one-one onto
(d) into

Answer

Answer: (c) one-one onto

---

Question 6.
The period of sin² θ is
(a) π²
(b) π
(c) 2π
(d) \(\frac{π}{2}\)

Answer

Answer: (b) π

---

Question 7.
f(x) = \(\frac{log_2(x+3)}{x^2+3x+2}\) is the domain of
(a) R – {-1, -2}
(b) (- 2, ∞) .
(c) R- {- 1,-2, -3}
(d) (-3, + ∞) – {-1, -2}

Answer

Answer: (d) (-3, + ∞) – {-1, -2}

---

Question 8.
Let P = {(x, y) | x² + y² = 1, x, y ∈ R]. Then, P is
(a) Reflexive
(b) Symmetric
(c) Transitive
(d) Anti-symmetric

Answer

Answer: (b) Symmetric

---

Question 9.
The relation R is defined on the set of natural numbers as {(a, b): a = 2b}. Then, R^-1 is given by
(a) {(2, 1), (4, 2), (6, 3),….}
(b) {(1, 2), (2, 4), (3, 6),….}
(c) R^-1 is not defined
(d) None of these

Answer

Answer: (b) {(1, 2), (2, 4), (3, 6),….}

---

Question 10.
The relation R = {(1,1), (2, 2), (3, 3), (1, 2), (2, 3), (1, 3)} on set A = {1, 2, 3} is
(a) Reflexive but not symmetric
(b) Reflexive but not transitive
(c) Symmetric and transitive
(d) Neither symmetric nor transitive

Answer

Answer: (a) Reflexive but not symmetric

---

Question 11.
The identity element for the binary operation * defined on Q ~ {0} as
a * b = \(\frac{ab}{2}\) ∀ a, b ∈ Q ~ {0} is
(a) 1
(b) 0
(c) 2
(d) None of these

Answer

Answer: (c) 2

---

Question 12.
Let f : R → R be defined by f (x) = \(\frac{1}{x}\) ∀ x ∈ R. Then f is
(a) one-one
(b) onto
(c) bijective
(d) f is not defined

Answer

Answer: (d) f is not defined

---

Question 13.
Consider the non-empty set consisting of children is a family and a relation R defined as aRb If a is brother of b. Then R is
(a) symmetric but not transitive
(b) transitive but not symmetric
(c) neither symmetric nor transitive
(d) both symmetric and transitive

Answer

Answer: (b) transitive but not symmetric

---

Question 14.
Let us define a relation R in R as aRb if a ≥ b. Then R is
(a) an equivalence relation
(b) reflexive, transitive but not symmetric
(c) neither transitive nor reflexive but symmetric
(d) symmetric, transitive but not reflexive

Answer

Answer: (b) reflexive, transitive but not symmetric

---

Question 15.
Let f: A → B and g : B → C be the bijective functions. Then (g o f)^-1 is,
(a) f^-1 o g^-1
(b) f o g
(c ) g^-1 o f^-1
(d) g o f

Answer

Answer: (a) f^-1 o g^-1

---

Question 16.
Let f: [0, 1| → [0, 1| be defined by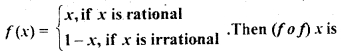

(a) Constant
(b) 1 + x
(c) x
(d) None of these

Answer

Answer: (c) x

---

Question 17.
Let R be a relation on the set N of natural numbers denoted by nRm ⇔ n is a factor of m (i.e. n | m). Then, R is
(a) Reflexive and symmetric
(b) Transitive and symmetric
(c) Equivalence
(d) Reflexive, transitive but not symmetric

Answer

Answer: (d) Reflexive, transitive but not symmetric

---

Question 18.
What type of a relation is R = {(1, 3), (4, 2), (2, 4), (2, 3), (3, 1)} on the set A – {1, 2, 3, 4}
(a) Reflexive
(b) Transitive
(c) Symmetric
(d) None of these

Answer

Answer: (d) None of these

---

Question 19.
Consider the binary operation * on a defined by x * y = 1 + 12x + xy, ∀ x, y ∈ Q, then 2 * 3 equals
(a) 31
(b) 40
(c) 43
(d) None of these

Answer

Answer: (a) 31

---

Question 20.
The range of the function f(x) = \(\sqrt{(x-1)(3-x)}\) is
(a) [1, 3]
(b) [0, 1]
(c) [-2, 2]
(d) None of these

Answer

Answer: (a) [1, 3]

---

Question 21.
Let A = {1, 2, 3, 4,…. n} How many bijective function f : A → B can be defined?
(a) \(\frac{1}{2}\)n

(d) n

Answer

Answer: (c) [n

---

Question 22.
If A = (1, 2, 3}, B = {6, 7, 8} is a function such that f(x) = x + 5 then what type of a function is f?
(a) Many-one onto
(b) Constant function
(c) one-one onto
(d) into

Answer

Answer: (c) one-one onto

---

Question 23.
What type of relation is ‘less than’ in the set of real numbers?
(a) only symmetric
(b) only transitive
(c) only reflexive
(d) equivalence

Answer

Answer: (b) only transitive

---

Question 24.
f: A → B will be an into function if
(a) range (f) ⊂ B
(b) f(a) = B
(c) B ⊂ f(a)
(d) f(b) ⊂ A

Answer

Answer: (a) range (f) ⊂ B

---

Question 25.
Let T be the set of all triangles in the Euclidean plane, and let a relation R on T be defined as aRb if a congruent to b ∀ a, b ∈ T. Then R is
(a) reflexive but-not transitive
(b) transitive but not symmetric
(c) equivalence
(d) None of these

Answer

Answer: (c) equivalence

---

Question 26.
The maximum number of equivalence relations on the set A = {1, 2, 3} are
(a) 1
(b) 2
(c) 3
(d) 5

Answer

Answer: (d) 5

---

Question 27.
Let R be an equivalence relation on a finite set A having n elements. Then, the number of ordered pairs in R is
(a) Less than n
(b) Greater than or equal to n
(c) Less than or equal to n
(d) None of these

Answer

Answer: (b) Greater than or equal to n

---

Question 28.
Let f: R – {\(\frac{3}{5}\)} → R be defined by f(x) = \(\frac{3x+2}{5x-3}\) then
(a) f^-1(x) = f(x)
(b) f^-1(x) = -f(x)
(c ) (f o f)x = -x
(d ) f^-1(x) = \(\frac{1}{19}\) f(x)

Answer

Answer: (a) f^-1(x) = f(x)

---

Question 29.
Which of the following functions from Z into Z are bijective?
(a) f(x) = x³
(b) f(x) = x + 2
(c) f(x) = 2x + 1
(d) f{x) = x² + 1

Answer

Answer: (b) f(x) = x + 2

---

Question 30.
If f(x₁) = f (x₂) ⇒ x₁ = x₂ ∀ x₁ x₂ ∈ A then the function f: A → B is
(a) one-one
(b) one-one onto
(c) onto
(d) many one

Answer

Answer: (a) one-one

---