CBSE Class 10 Maths – MCQ and Online Tests – Unit 8 – Introduction to Trigonometry
Every year CBSE conducts board exams for 10th standard. These exams are very competitive to all the students. So our website provides online tests for all the 10th subjects. These tests are also very effective and useful for those who preparing for competitive exams like NEET, JEE, CA etc. It can boost their preparation level and confidence level by attempting these chapter wise online tests.
These online tests are based on latest CBSE Class 10 syllabus. While attempting these our students can identify the weak lessons and continuously practice those lessons for attaining high marks. It also helps to revise the NCERT textbooks thoroughly.
CBSE Class 10 Maths – MCQ and Online Tests – Unit 1 – Introduction to Trigonometry
Question 1.
Given that sin θ = \(\frac{a}{b}\) then cos θ is equal to
(a) \(\frac{b}{\sqrt{b^2-a^2}}\)
(b) \(\frac{b}{a}\)
(c) \(\frac{\sqrt{b^2-a^2}}{b}\)
(d) \(\frac{a}{\sqrt{b^2-a^2}}\)
Answer
Answer: (c) \(\frac{\sqrt{b^2-a^2}}{b}\)
Question 2.
Given that sin α = \(\frac{1}{2}\) and cos β = \(\frac{1}{2}\), then the value of (α + β) is
(a) 0°
(b) 30°
(c) 60°
(d) 90°
Answer
Answer: (d) 90°
Question 3.
If tan θ = 3, then \(\frac{4sin θ-cos θ }{4sin θ+cos θ}\) is equal to
(a) \(\frac{2}{3}\)
(b) \(\frac{1}{3}\)
(c) \(\frac{1}{2}\)
(d) \(\frac{3}{4}\)
Answer
Answer: (c) \(\frac{1}{2}\)
Question 4.
sin (45° + θ) – cos (45° – θ) is equal to
(a) 2 cos θ
(b) 0
(c) 2 sin θ
(d) 1
Answer
Answer: (b) 0
Question 5.
If √2 sin (60° – α) = 1 then α is
(a) 45°
(b) 15°
(c) 60°
(d) 30°
Answer
Answer: (b) 15°
Question 6.
The value of sin² 30° – cos² 30° is
(a) –\(\frac{1}{2}\)
(b) \(\frac{√3}{2}\)
(c) \(\frac{3}{2}\)
(d) –\(\frac{2}{3}\)
Answer
Answer: (a) –\(\frac{1}{2}\)
Question 7.
The maximum value of \(\frac{1}{cosec α}\) is
(a) 0
(b) 1
(c) \(\frac{√3}{2}\)
(d) –\(\frac{1}{√2}\)
Answer
Answer: (b) 1
Question 8.
If cos (40° + A) = sin 30°, then value of A is
(a) 30°
(b) 40°
(c) 60°
(d) 20°
Answer
Answer: (d) 20°
Question 9.
If cosec θ – cot θ = \(\frac{1}{3}\), the value of (cosec θ + cot θ) is
(a) 1
(b) 2
(c) 3
(d) 4
Answer
Answer: (c) 3
Question 10.
In the given figure, if AB = 14 cm, BD = 10 cm and DC = 8 cm, then the value of tan B is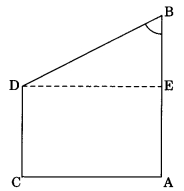
(a) \(\frac{4}{3}\)
(b) \(\frac{14}{3}\)
(c) \(\frac{5}{3}\)
(d) \(\frac{13}{3}\)
Answer
Answer: (a) \(\frac{4}{3}\)
Question 11.
\(\frac{1+tan^2 A}{1+cot^2 A}\) is equal to
(a) sec² A
(b) -1
(c) cot² A
(d) tan² A
Answer
Answer: (d) tan² A
Question 12.
If cos A + cos² A = 1, then sin² A + sin4 A is equal to
(a) -1
(b) 0
(c) 1
(d) None of these
Answer
Answer: (c) 1
Question 13.
If sin θ + sin² θ = 1 then cos² θ + cos4 θ is equal
(a) -1
(b) 1
(c) 0
(d) None of these
Answer
Answer: (b) 1
Question 14.
2(sin6 θ + cos6 θ) – 3(sin4 θ + cos4 θ) is equal to
(a) 0
(b) 6
(c) -1
(d) None of these
Answer
Answer: (c) -1
Question 15.
If cos (81 + θ)° = sin(\(\frac{k}{3}\) – θ)° where θ is an acute angle, then the value of k is
(a) 18°
(b) 27°
(c) 9°
(d) 81°
Answer
Answer: (b) 27°
Question 16.
3 sin² 20° – 2 tan² 45° + 3 sin² 70° is equal to
(a) 0
(b) 1
(c) 2
(d) -1
Answer
Answer: (b) 1
Question 17.
If sin 2A = \(\frac{1}{2}\) tan² 45° where A is an acute angle, then the value of A is
(a) 60°
(b) 45°
(c) 30°
(d) 15°
Answer
Answer: (d) 15°
Question 18.
\(\frac{sin θ}{1 + cos θ}\) is
(a) \(\frac{cos θ}{1 – sin θ}\)
(b) \(\frac{1 – sin θ}{sin θ}\)
(c) \(\frac{1 – sin θ}{cos θ}\)
(d) \(\frac{1 – cos θ}{sin θ}\)
Answer
Answer: (d) \(\frac{1 – cos θ}{sin θ}\)
Question 19.
If x sin (90° – θ) cot (90° – θ) = cos (90° – θ), then x is equal to
(a) 0
(b) 1
(c) -1
(d) 2
Answer
Answer: (b) 1
Question 20.
If A + B = 90°, cot B = \(\frac{3}{4}\) then tan A is equal to:
(a) \(\frac{5}{3}\)
(b) \(\frac{1}{3}\)
(c) \(\frac{3}{4}\)
(d) \(\frac{1}{4}\)
Answer
Answer: (c) \(\frac{3}{4}\)













0 Comments:
Post a Comment