CBSE Class 9 Maths – MCQ and Online Tests – Unit 4 – Linear Equations for Two Variables
Every year CBSE schools conducts Annual Assessment exams for 6,7,8,9,11th standards. These exams are very competitive to all the students. So our website provides online tests for all the 6,7,8,9,11th standard’s subjects. These tests are also very effective and useful for those who preparing for any competitive exams like Olympiad etc. It can boost their preparation level and confidence level by attempting these chapter wise online tests.
These online tests are based on latest CBSE syllabus. While attempting these our students can identify the weak lessons and continuously practice those lessons for attaining high marks. It also helps to revise the NCERT textbooks thoroughly.
CBSE Class 9 Maths – MCQ and Online Tests – Unit 4 – Linear Equations for Two Variables
Question 1.
Which of the following ordered pairs is a solution of the equation x – 2y – 6?
(a) (2, 4)
(b) (0, 3)
(c) (-4, 1)
(d) (4, -1)
Answer
Answer: (d) (4, -1)
Question 2.
Which of the following is the equation of a line parallel to y-axis?
(a) y = 0
(b) x + y = z
(c) y = x
(d) x = a
Answer
Answer: (d) x = a
Question 3.
Any point on the line y = 3x is of the form
(a) (a, 3a)
(b) (3a, a)
(c) (a, \(\frac{a}{3}\))
(d) (\(\frac{a}{3}\), -a)
Answer
Answer: (a) (a, 3a)
Question 4.
To which equation does the graph represent?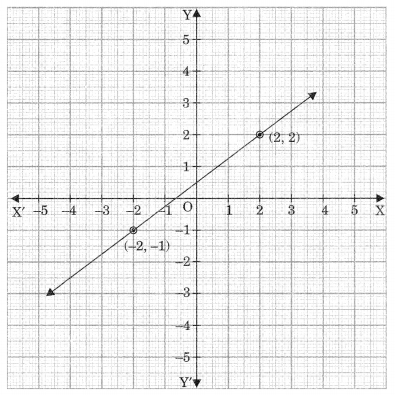
(a) 3x – 7y = 10
(b) y – 2x = 3
(c) 8y – 6x = 4
(d) 5x +\(\frac{35}{2}\)y = 25
Answer
Answer: (c) 8y – 6x = 4
Question 5.
Any point of the form (a, – a) always lie on the graph of the equation
(a) x = -a
(b) y = a
(c) y = x
(d) x + y = 0
Answer
Answer: (d) x + y = 0
Question 6.
The graph of the equation 2x + 3y = 6 cuts the x-axis at the point
(a) (0, 3)
(b) (3, 0)
(c) (2, 0)
(d) (0, 2)
Answer
Answer: (b) (3, 0)
Question 7.
Graph of linear equation ax + by + c = 0, a * 0, 6*0 cuts x-axis and y-axis respectively at the points.
(a) (\(\frac{-c}{a}\), 0), (0, \(\frac{-c}{b}\))
(b) (0, \(\frac{-c}{b}\), 0), (\(\frac{-c}{a}\), 0)
(c) (-c, 0) (0, -c)
(d) (x, 0) (y, 0)
Answer
Answer: (a) (\(\frac{-c}{a}\), 0), (0, \(\frac{-c}{b}\))
Question 8.
Equation of a line which is 5 units distance above the x-axis is
(a) x = 5
(b) x + 5 = y
(c) y – 5
(d) x – y = 0
Answer
Answer: (c) y – 5
Question 9.
How many linear equation in x and y can be satisfied by x = 1 and y = 2?
(a) only one
(b) two
(c) infinitely many
(d) three
Answer
Answer: (c) infinitely many
Question 10.
Solution of linear equation 2x + 0.y + 9 = 0 is
(a) (\(\frac{9}{2}\), m)
(b) (n, \(\frac{-9}{2}\))
(c) (0, \(\frac{-9}{2}\))
(d) (\(\frac{-9}{2}\), 0)
Answer
Answer: (d) (\(\frac{-9}{2}\), 0)
Question 11.
The maximum number of points that lie on the graph of a linear equation in two variables is.
(a) two
(b) definite
(c) infinitely many
(d) three
Answer
Answer: (c) infinitely many
Question 12.
If (3, 2) is the solution 3x – ky = 5, then k equals of the equation
(a) 2
(b) 4
(c) 3
(d) \(\frac{1}{2}\)
Answer
Answer: (a) 2
Question 13.
Cost of book (x) exceeds twice the cost of pen (y) by Rs 10. This statement can be expressed as linear equation.
(a) x – 2y – 10 = 0
(b) 2x – y – 10 = 0
(c) 2x + y – 10 = 0
(d) x – 2y + 10 = 0
Answer
Answer: (a) x – 2y – 10 = 0
Question 14.
If x represents the age of father and y represents the present age of the son, then the statement for ‘present age of father is 5 more than 6 times the age of the son’ in terms of mathematical equation is
(a) 6x + y = 5
(b) x = 6y + 5
(c) x + 6y = 5
(d) x – 6 = 5
Answer
Answer: (b) x = 6y + 5
Question 15.
Equation of a line passing through origin is
(a) x + y = 1
(b) x = 2y – 4
(c) x + y = 0
(d) y = x – 1
Answer
Answer: (c) x + y = 0
Question 16.
The condition that the equation ax + by + c = 0 represents a linear equation in two variables is
(a) a ? 0, b = 0
(b) b ? 0, a = 0
(c) a = 0, b = 0
(d) a ? 0, b ? 0
Answer
Answer: (d) a ? 0, b ? 0
Question 17.
x = 3 and y = -2 is a solution of the equation 4px – 3y = 12, then the value of p is
(a) 0
(b) \(\frac{1}{2}\)
(c) 2
(d) 3
Answer
Answer: (b) \(\frac{1}{2}\)














0 Comments:
Post a Comment