CBSE Class 6 Maths - MCQ and Online Tests - Unit 14 - Practical Geometry

CBSE Class 6 Maths – MCQ and Online Tests – Unit 14 – Practical Geometry

Every year CBSE students attend Annual Assessment exams for 6,7,8,9,11th standards. These exams are very competitive to all the students. So our website provides online tests for all the 6,7,8,9,11th standards’ subjects. These tests are also very effective and useful for those who preparing for any competitive exams like Olympiad etc. It can boost their preparation level and confidence level by attempting these chapter wise online tests.

These online tests are based on latest CBSE syllabus. While attempting these, our students can identify their weak lessons and continuously practice those lessons for attaining high marks. It also helps to revise the NCERT textbooks thoroughly.

CBSE Class 6 Maths – MCQ and Online Tests – Unit 14 – Practical Geometry

Question 1.
If two lines have only one point in common, what are they called?
(a) Parallel lines
(b) Intersecting lines
(c) Perpendicular lines
(d) Transversal

Answer

Answer: (b) Intersecting lines
Hint:
Intersecting lines have only one point in common.

---

Question 2.
\(\overrightarrow { MN }\) is the perpendicular bisector of \(\overleftrightarrow { AB }\). Which of the given statements is correct?
(i) ∠ANM + ∠MNB = 90∘
(ii) \(\overline { AN }\) = \(\overline { NB }\)
(iii) \(\overline { AN }\) = 2 \(\overline { NB }\)
(iv) ∠MNB = \(\frac{1}{2}\) ∠ANM
(a) (i) and (iii) only
(b) (ii) and (iv) only
(c) (i) and (ii) only
(d) (ii) and (iii) only

Answer

Answer: (c) (i) and (ii) only
Hint:
\(\overrightarrow { NM }\) ⊥ \(\overleftrightarrow { AB }\) and \(\overrightarrow { NM }\) divides \(\overleftrightarrow { AB }\) into two congruent parts.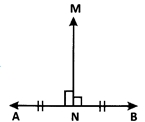

Clearly ∠ANM = ∠MNB = 90∘ is true. \(\overline { AN }\) = \(\overline { NB }\) is true since \(\overrightarrow { NM }\) ⊥ \(\overleftrightarrow { AB }\), \(\overline { AN }\) = 2\(\overline { NB }\) is false, and ∠MNB = \(\frac{1}{2}\) ∠ANM is false. Thus, only (i) and (ii) are correct.

---

Question 3.
Which of the following can be drawn on a piece of paper?
(a) A line
(b) A line segment
(c) A ray
(d) A plane

Answer

Answer: (b) A line segment

---

Question 4.
Identify the uses of a ruler.
(a) To draw a line segment of a given length
(b) To draw a copy of a given segment.
(c) To draw a diameter of a circle.
(d) All the above.

Answer

Answer: (d) All the above.
Hint:
A ruler is used to draw a line segment of a given length, to draw the copy of a given segment, and to draw a diameter of a circle. Thus, all the given options are correct.

---

Question 5.
P is the midpoint of \(\overline { AB }\). M and N are midpoints of \(\overline { AP }\) respectively. What is the measure of \(\overline { MN }\)?
(a) \(\frac{1}{3}\) \(\overline { AB }\)
(b) \(\frac{1}{2}\) \(\overline { AB }\)
(c) \(\frac{1}{2}\) \(\overline { AP }\)
(d) \(\frac{3}{2}\) \(\overline { AB }\)

Answer

Answer: (b) \(\frac{1}{2}\) \(\overline { AB }\)
Hint:

P is the midpoint of \(\overline { AB }\) ⇒ AP = PB M and N are midpoints of \(\overline { AP }\) and \(\overline { PB }\) ⇒ \(\overline { AM }\) = \(\overline { MP }\) and \(\overline { PN }\) = \(\overline { NB }\)
∴ \(\overline { MN }\) = \(\overline { MP }\) + \(\overline { PN }\) = \(\frac{1}{2}\) \(\overline { AP }\) + \(\frac{1}{2}\) \(\overline { PB }\) = \(\frac{1}{2}\) (\(\overline { AP }\) + \(\overline { PB }\) ) = \(\frac{1}{2}\) (\(\overline { AB }\))

---

Question 6.
\(\overrightarrow { XY }\) bisects∠AXB. If ∠YXB = 37.5∘, what is the measure of ∠AXB?
(a) 37.5°
(b) 74°
(c) 64°
(d) 75°

Answer

Answer: (d) 75°

---

Question 7.
\(\overrightarrow { XY }\) divides ∠MXN = 72° in the ratio 1 : 2. What is the measure of ∠YXN?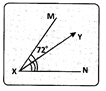

(a) 48°
(b) 24°
(c) 72°
(d) 96°

Answer

Answer: (a) 48°
Hint: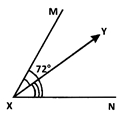

Given ∠MXN = 72∘ and \(\overrightarrow { XY }\) divides ∠MXN in the ratio 1 : 2.
∠YXN = \(\frac{2}{3}\) ∠MXN = \(\frac{2}{3}\) × 72° = 48°

---

Question 8.
X and Y are two distinct points in a plane. How many lines can be drawn passing through both X and Y?
(a) 0
(b) 1
(c) Only 2
(d) Infinitely many

Answer

Answer: (b) 1

---

Question 9.
l || m. P and Q are points on land m respectively such that PQ ⊥ lR is a point on a line n in the same plane such that \(\overline { PQ }\) = \(\overline { QR }\). Which of the following is true?
(a) l || n
(b) m || n
(c) Both [a] and [b]
(d) Neither [a] nor [b]

Answer

Answer: (c) Both [a] and [b]
Hint: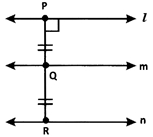

Clearly, from the given data and the figure, l || n and m || n.

---

Question 10.
Lines a, b, p, q, m, n and x have a point P common to all of them. What is the name of P?
(a) Point of concurrence
(b) Point of intersection
(c) Common point
(d) Distinct point

Answer

Answer: (a) Point of concurrence
Hint:
A point common to multiple lines is called a point of concurrence as the lines are concurrent lines.

---

Question 11.
\(\overrightarrow { QZ }\) is the bisector of ∠PQZ = ∠PQR. Which of the following is true?
(a) ∠PQZ = ∠PQR
(b) ∠PQZ = ∠ZQR
(c) ∠PQZ = \(\frac{1}{2}\) ∠ZQR
(d) Both [b] and [c]

Answer

Answer: (d) Both [b] and [c]
Hint:
\(\overrightarrow { QZ }\) bisects ∠PQR (Given)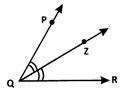

Thus. ∠PQZ = ∠ZQR = \(\frac{1}{2}\) ∠PQR

---

Question 12.
At 7 a.m. the angle between the Sun’s ray and the ground at a point is 43°. What would be the angle at 10 a.m.?
(a) 40°
(b) 90°
(c) Between 43° and 90°
(d) Greater than 90°

Answer

Answer: (c) Between 43° and 90°
Hint: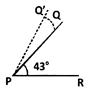

Let QP be the sun’s ray and RP be the ground. The angle between QP and PR at P is 43° at 7 a.m. At 10 a.m., the sun’s ray is Q’P. We know that at 12 noon the sun is exactly above our head. So, the sun’s ray will be perpendicular to the ground. So, clearly at 10 am, the required angle will be between 43° and 90°.

---

Question 13.
Identify the pair of parallel lines.
(i) Lines m and n have two points in common.
(ii) Lines p and q do not have any point in common
(iii) Lines p and q have a point X in common.
(a) (i) and (ii) only
(b) (ii) only
(c) (ii) and (iii) only
(d) (i), (ii) and (iii)

Answer

Answer: (b) (ii) only
Hint:
Parallel lines do not have any point in common.

---

Question 14.
A line segment \(\overrightarrow { TP } \) is bisected at I. What is the measure of \(\overrightarrow { TI }\)?
(a) \(\frac{1}{2}\)\(\overrightarrow { TP }\)
(b) \(\overrightarrow { IP }\)
(c) \(\overrightarrow { TP }\)
(d) \(\frac{1}{3}\) \(\overrightarrow { TP }\)

Answer

Answer: (b) \(\overrightarrow { IP }\)
Hint:
\(\overrightarrow { TI }\) = \(\frac{1}{3}\) \(\overrightarrow { TP }\) = IP

---

Question 15.
Identify the one with no definite length.
(a) \(\overleftrightarrow { AB }\)
(b) \(\overline { PQ }\)
(c) -XYZ
(d) \(\overline { MN }\)

Answer

Answer: (a) \(\overleftrightarrow { AB }\)
Hint:
\(\overleftrightarrow { AB }\) has no definite length.

---