CBSE Class 11 Maths – MCQ and Online Tests – Unit 1 – Sets
Every year CBSE schools conducts Annual Assessment exams for 6,7,8,9,11th standards. These exams are very competitive to all the students. So our website provides online tests for all the 6,7,8,9,11th standard’s subjects. These tests are also very effective and useful for those who preparing for any competitive exams like Olympiad etc. It can boost their preparation level and confidence level by attempting these chapter wise online tests.
These online tests are based on latest CBSE syllabus. While attempting these our students can identify the weak lessons and continuously practice those lessons for attaining high marks. It also helps to revise the NCERT textbooks thoroughly.
CBSE Class 11 Maths – MCQ and Online Tests – Unit 1 – Sets
Question 1.
If A, B, C be three sets such that A ? B = A ? C and A n B = A n C, then,
(a) B = C
(b) A = C
(c) A = B = C
(d) A = B
Answer
Answer: (a) B = C
Hint:
Given A, B, C be three sets such that A ? B = A ? C and A n B = A n C then B = C
Question 2.
In 2nd quadrant?
(a) X < 0, Y < 0
(b) X < 0, Y > 0
(c) X > 0, Y > 0
(d) X > 0, Y < 0
Answer
Answer: (b) X < 0, Y > 0
Hint:
In the second quadrant,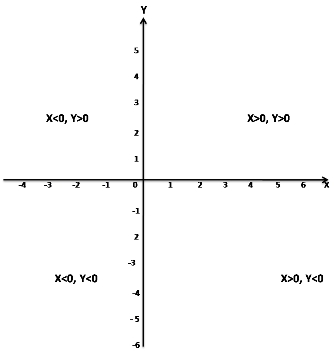
X < 0, Y > 0
Question 3.
A – B is read as?
(a) Difference of A and B of B and A
(b) None of the above
(c) Difference of B and A
(d) Both a and b
Answer
Answer: (a) Difference of A and B of B and A
Hint:
A – B will read as difference of A and B of B and A
Ex: Let A = {1, 2, 3, 4, 5} and B = {1, 3, 5, 7}
Now, A – B = {2, 4}
Question 4.
If A, B and C are any three sets, then A × (B ? C) is equal to
(a) (A × B) ? (A × C)
(b) (A ? B) × (A ? C)
(c) None of these
(d) (A × B) n (A × C)
Answer
Answer: (a) (A × B) ? (A × C)
Hint:
Given A, B and C are any three sets.
Now, A × (B ? C) = (A × B) ? (A × C)
Question 5.
IF A = [5, 6, 7] and B = [7, 8, 9] then A ? B is equal to
(a) [5, 6, 7, 8, 9]
(b) [5, 6, 7]
(c) [7, 8, 9]
(d) None of these
Answer
Answer: (a) [5, 6, 7, 8, 9]
Hint:
Given A = [5, 6, 7] and B = [7, 8, 9]
then A ? B = [5, 6, 7, 8, 9]
Question 6.
Which of the following sets are null sets
(a) {x: |x |< -4, x ?N}
(b) 2 and 3
(c) Set of all prime numbers between 15 and 19
(d) {x: x < 5, x > 6}
Answer
Answer: (b) 2 and 3
Hint:
2 and 3 is the null set.
Question 7.
IF R = {(2, 1),(4, 3),(4, 5)}, then range of the function is?
(a) Range R = {2, 4}
(b) Range R = {1, 3, 5}
(c) Range R = {2, 3, 4, 5}
(d) Range R {1, 1, 4, 5}
Answer
Answer: (b) Range R = {1, 3, 5}
Hint:
Given R = {(2, 1),(4, 3),(4, 5)}
then Range(R) = {1, 3, 5}
Question 8.
If A, B and C are any three sets, then A – (B ? C) is equal to
(a) (A – B) ? (A – C)
(b) (A – B) ? C
(c) (A – B) n C
(d) (A – B) n (A – C)
Answer
Answer: (d) (A – B) n (A – C)
Hint:
Given A, B and C are any three sets.
Now, A – (B ? C) = (A – B) n (A – C)
Question 9.
(A’)’ = ?
(a) ? – A
(b) A’
(c) ?
(d) A
Answer
Answer: (d) A
Hint:
(A’)’ = A
Question 10.
{ (A, B) : A² +B² = 1} on the sets has the following relation
(a) reflexive
(b) symmetric
(c) none
(d) reflexive and transitive
Answer
Answer: (b) symmetric
Hint:
Given {(a, b) : a² + b² = 1} on the set S.
Now a² +b² = b² + a² = 1
So, the given relation is symmetric.
Question 11.
Two finite sets have N and M elements. The number of elements in the power set of first set is 48 more than the total number of elements in power set of the second test. Then the value of M and N are
(a) 7, 6
(b) 6, 4
(c) 7, 4
(d) 6, 3
Answer
Answer: (b) 6, 4
Hint:
Let A and B be two sets having m and n numbers of elements respectively
Number of subsets of A = 2m
Number of subsets of B = 2n
Now, according to question
2m – 2n = 48
? 2n(2m – n – 1) = 24(22 – 1)
So, n = 4
and m – n = 2
? m – 4 = 2
? m = 2 + 4
? m = 6
Question 12.
In a class of 120 students numbered 1 to 120, all even numbered students opt for Physics, whose numbers are divisible by 5 opt for Chemistry and those whose numbers are divisible by 7 opt for Math. How many opt for none of the three subjects?
(a) 19
(b) 41
(c) 21
(d) 57
Answer
Answer: (b) 41
Hint:
The number of students who took at least one of the three subjects can be found by finding out A ? B ? C, where A is the set of those who took Physics, B the set of those who took Chemistry and C the set of those who opted for Math.
Now, A ? B ? C = A + B + C – (A n B + B n C + C n A) + (A n B n C)
A is the set of those who opted for Physics = 120/2 = 60 students
B is the set of those who opted for Chemistry = 120/5 = 24
C is the set of those who opted for Math = 120/7 = 17
The 10th, 20th, 30th….. numbered students would have opted for both Physics and Chemistry.
Therefore, A n B = 120/10 = 12
The 14th, 28th, 42nd….. Numbered students would have opted for Physics and Math.
Therefore, C n A = 120/14 = 8
The 35th, 70th…. numbered students would have opted for Chemistry and Math.
Therefore, B n C = 120/35 = 3
And the 70th numbered student would have opted for all three subjects.
Therefore, A ? B ? C = 60 + 24 + 17 – (12 + 8 + 3) + 1 = 79
Number of students who opted for none of the three subjects = 120 – 79 = 41
Question 13.
The range of the function f(x) = 3x – 2‚ is
(a) (- 8, 8)
(b) R – {3}
(c) (- 8, 0)
(d) (0, – 8)
Answer
Answer: (a) (- 8, 8)
Hint:
Let the given function is
y = 3x – 2
? y + 2 = 3x
? x = (y + 2)/3
Now x is saisfied by all values.
So, Range{f(x)} = R = (-8, 8)
Question 14.
In a class of 50 students, 10 did not opt for math, 15 did not opt for science and 2 did not opt for either. How many students of the class opted for both math and science.
(a) 24
(b) 25
(c) 26
(d) 27
Answer
Answer: (d) 27
Hint:
Total students = 50
Students who did not opt for math = 10
Students who did not opt for Science = 15
Students who did not opt for either maths or science = 2
Total of 40 students in math and 13 did not opt for science but did for math = 40 – 13 = 27
So, students of the class opted for both math and science is 27
Question 15.
In last quadrant?
(a) X < 0, Y > 0
(b) X < 0, Y < 0
(c) X > 0, Y < 0
(d) X > 0, Y > 0
Answer
Answer: (d) X > 0, Y > 0
Hint:
In the last quadrant,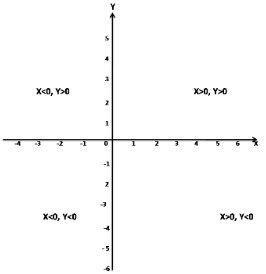
X > 0, Y > 0
Question 16.
How many rational and irrational numbers are possible between 0 and 1?
(a) 0
(b) Finite
(c) Infinite
(d) 1
Answer
Answer: (c) Infinite
Hint:
There are infinite many rational and irrational numbers are possible between 0 and 1
This is because between any two numbers, there are infinite numbers.
Question 17.
Empty set is a?
(a) Finite Set
(b) Invalid Set
(c) None of the above
(d) Infinite Set
Answer
Answer: (a) Finite Set
Hint:
In mathematics, and more specifically set theory, the empty set is the unique set having no elements and its size or cardinality (count of elements in a set) is zero.
So, an empty set is a finite set.
Question 18.
If A = [5, 6, 7] and B = [7, 8, 9] then A U B is equal to
(a) [5, 6, 7, 8, 9]
(b) [5, 6, 7]
(c) [7, 8, 9]
(d) None of these
Answer
Answer: (a) [5, 6, 7, 8, 9]
Hint:
Given A = [5, 6, 7] and B = [7, 8, 9]
then A U B = [5, 6, 7, 8, 9]
Question 19.
Which of the following two sets are equal?
(a) A = {1, 2} and B = {1}
(b) A = {1, 2} and B = {1, 2, 3}
(c) A = {1, 2, 3} and B = {2, 1, 3}
(d) A = {1, 2, 4} and B = {1, 2, 3}
Answer
Answer: (c) A = {1, 2, 3} and B = {2, 1, 3}
Hint:
Two sets are equal if and only if they have the same elements.
So, A = {1, 2, 3} and B = {2, 1, 3} are equal sets.
Question 20.
The members of the set S = {x | x is the square of an integer and x < 100} is
(a) {0, 2, 4, 5, 9, 58, 49, 56, 99, 12}
(b) {0, 1, 4, 9, 16, 25, 36, 49, 64, 81}
(c) {1, 4, 9, 16, 25, 36, 64, 81, 85, 99}
(d) {0, 1, 4, 9, 16, 25, 36, 49, 64, 121}
Answer
Answer: (b) {0, 1, 4, 9, 16, 25, 36, 49, 64, 81}
Hint:
The set S consists of the square of an integer less than 100
So, S = {0, 1, 4, 9, 16, 25, 36, 49, 64, 81}














0 Comments:
Post a Comment