CBSE Class 11 Maths – MCQ and Online Tests – Unit 11 – Conic Sections
Every year CBSE schools conducts Annual Assessment exams for 6,7,8,9,11th standards. These exams are very competitive to all the students. So our website provides online tests for all the 6,7,8,9,11th standard’s subjects. These tests are also very effective and useful for those who preparing for any competitive exams like Olympiad etc. It can boost their preparation level and confidence level by attempting these chapter wise online tests.
These online tests are based on latest CBSE syllabus. While attempting these our students can identify the weak lessons and continuously practice those lessons for attaining high marks. It also helps to revise the NCERT textbooks thoroughly.
CBSE Class 11 Maths – MCQ and Online Tests – Unit 11 – Conic Sections
Question 1.
The radius of the circle 4x² + 4y² – 8x + 12y – 25 = 0 is?
(a) v57/4
(b) v77/4
(c) v77/2
(d) v87/4
Answer
Answer: (c) v77/2
Hint:
Given, equation fo the of the circle is 4x² + 4y² – 8x + 12y – 25 = 0
? x² + y² – 8x/4 + 12y/4 – 25/4 = 0
? x² + y² – 2x + 3y – 25/4 = 0
Now, radius = v{(-2)² + (3)² – (-25/4)}
= v{4 + 9 + 25/4}
= v{13 + 25/4}
= v{(13×4 + 25)/4}
= v{(52 + 25)/4}
= v{77/4}
= v77/2
Question 2.
If (a, b) is the mid point of a chord passing through the vertex of the parabola y² = 4x, then
(a) a = 2b
(b) 2a = b
(c) a² = 2b
(d) 2a = b²
Answer
Answer: (d) 2a = b²
Hint:
Let P(x, y) be the coordinate of the other end of the chord OP where O(0, 0)
Now, (x + 0)/2 = a
? x = 2a
and (y + 0)/2 = b
? y = 2b
Now, y² = 4x
? (2b)² = 4 × 2a
? 4b² = 8a
? b² = 2a
Question 3.
A man running a race course notes that the sum of the distances from the two flag posts from him is always 10 meter and the distance between the flag posts is 8 meter. The equation of posts traced by the man is
(a) x²/9 + y²/5 = 1
(b) x²/9 + y2 /25 = 1
(c) x²/5 + y²/9 = 1
(d) x²/25 + y²/9 = 1
Answer
Answer: (d) x²/25 + y²/9 = 1
Hint: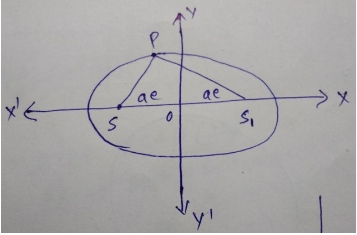
From the question, it is clear that the path traced by the man is an ellipse having its foci at two posts.
Let the equation of the ellipse be
x²/a² + y²/b² = 1
It is given that the sum of the distances of the man from the two flag posts is 10 m
This means that the sum of focal distances of a point on the ellipse is 10 m
? PS + PS1 = 10
? 2a = 10
? a = 5
Again, given that the distance between the flag posts is 8 meters
? 2ae = 8
? ae = 4
Now, b² = a² (1 – e²)
? b² = a² – a² e²
? b² = a² – (ae)²
? b² = 5² – 4²
? b² = 25 – 16
? b² = 9
? b = 3
Hence, the equation of the path is x²/5² + y²/3² = 1
? x²/25 + y²/9 = 1
Question 4.
The center of the ellipse (x + y – 2)² /9 + (x – y)² /16 = 1 is
(a) (0, 0)
(b) (0, 1)
(c) (1, 0)
(d) (1, 1)
Answer
Answer: (d) (1, 1)
Hint:
The center of the given ellipse is the point of intersection of the lines
x + y – 2 = 0 and x – y = 0
After solving, we get
x = 1, y = 1
So, the center of the ellipse is (1, 1)
Question 5.
The parametric coordinate of any point of the parabola y² = 4ax is
(a) (-at², -2at)
(b) (-at², 2at)
(c) (a sin²t, -2a sin t)
(d) (a sin t, -2a sin t)
Answer
Answer: (c) (a sin²t, -2a sin t)
Hint:
The point (a sin²t, -2a sin t) satisfies the equation of the parabola y² = 4ax for all
values of t. So, the parametric coordinate of any point of the parabola y² = 4ax is
(a sin²t, -2a sin t)
Question 6.
The equation of parabola with vertex at origin the axis is along x-axis and passing through the point (2, 3) is
(a) y² = 9x
(b) y² = 9x/2
(c) y² = 2x
(b) y² = 2x/9
Answer
Answer: (b) y² = 9x/2
Hint:
A parabola with its axis along the x-axis and vertex(0, 0) and direction x = -a has the equation:
y² = 4ax ………….. 1
Given, point (2,3) lies on the parabola,
? 3² = 4a × 2
? 9 = 4a × 2
? 9/2 = 4a
From equation 1, we get
y² = (9/2)x
? y² = 9x/2
This is the required equation of the parabola.
Question 7.
The locus of the point from which the tangent to the circles x² + y² – 4 = 0 and x² + y² – 8x + 15 = 0 are equal is given by the equation
(a) 8x + 19 = 0
(b) 8x – 19 = 0
(c) 4x – 19 = 0
(d) 4x + 19 = 0
Answer
Answer: (b) 8x – 19 = 0
Hint:
Given equation of circles are x² + y² – 4 = 0 and x² + y² – 8x + 15 = 0
Now, the required line is the radical axis of the two circles are
(x² + y² – 4) – (x² + y² – 8x + 15) = 0
? x² + y² – 4 – x² – y² + 8x – 15 = 0
? 8x – 19 = 0
Question 8.
The perpendicular distance from the point (3, -4) to the line 3x – 4y + 10 = 0
(a) 7
(b) 8
(c) 9
(d) 10
Answer
Answer: (a) 7
Hint:
The perpendicular distance = {3 × 3 – 4 × (-4) + 10}/v(3² + 4²)
= {9 + 16 + 10}/v(9 + 16)
= 35/v25
= 35/5
= 7
Question 9.
In an ellipse, the distance between its foci is 6 and its minor axis is 8 then its eccentricity is
(a) 4/5
(b) 1/v52
(c) 3/5
(d) 1/2
Answer
Answer: (c) 3/5
Hint:
Given, distance between foci = 6
? 2ae = 6
? ae = 3
Again minor axis = 8
? 2b = 8
? b = 4
? b² = 16
? a² (1 – e²) = 16
? a² – a² e² = 16
? a² – (ae)² = 16
? a² – 3² = 16
? a² – 9 = 16
? a² = 9 + 16
? a² = 25
? a = 5
Now, ae = 3
? 5e = 3
? e = 3/5
So, the eccentricity is 3/5
Question 10.
If the length of the tangent from the origin to the circle centered at (2, 3) is 2 then the equation of the circle is
(a) (x + 2)² + (y – 3)² = 3²
(b) (x – 2)² + (y + 3)² = 3²
(c) (x – 2)² + (y – 3)² = 3²
(d) (x + 2)² + (y + 3)² = 3²
Answer
Answer: (c) (x – 2)² + (y – 3)² = 3²
Hint:
Radius of the circle = v{(2 – 0)² + (3 – 0)² – 2²}
= v(4 + 9 – 4)
= v9
= 3
So, the equation of the circle = (x – 2)² + (y – 3)² = 3²
Question 11.
The equation of parabola whose focus is (3, 0) and directrix is 3x + 4y = 1 is
(a) 16x² – 9y² – 24xy – 144x + 8y + 224 = 0
(b) 16x² + 9y² – 24xy – 144x + 8y – 224 = 0
(c) 16x² + 9y² – 24xy – 144x – 8y + 224 = 0
(d) 16x² + 9y² – 24xy – 144x + 8y + 224 = 0
Answer
Answer: (d) 16x² + 9y² – 24xy – 144x + 8y + 224 = 0
Hint:
Given focus S(3, 0)
and equation of directrix is: 3x + 4y = 1
? 3x + 4y – 1 = 0
Let P (x, y) be any point on the required parabola and let PM be the length of the perpendicular from P on the directrix
Then, SP = PM
? SP² = PM²
? (x – 3)² + (y – 0)² = {(3x + 4y – 1) /{v(3² + 4²)}²
? x² + 9 – 6x + y² = (9x² + 16y² + 1 + 24xy – 8y – 6x)/25
? 25(x² + 9 – 6x + y²) = 9x² + 16y² + 1 + 24xy – 8y – 6x
? 25x² + 225 – 150x + 25y² = 9x² + 16y² + 1 + 24xy – 8y – 6x
? 25x² + 225 – 150x + 25y² – 9x² – 16y² – 1 – 24xy + 8y + 6x = 0
? 16x² + 9y² – 24xy – 144x + 8y + 224 = 0
This is the required equation of parabola.
Question 12.
The parametric representation (2 + t², 2t + 1) represents
(a) a parabola
(b) a hyperbola
(c) an ellipse
(d) a circle
Answer
Answer: (a) a parabola
Hint:
Let x = 2 + t²
? x – 2 = t² ……….. 1
and y = 2t + 1
? y – 1 = 2t
? (y – 1)/2 = t
From equation 1, we get
x – 2 = {(y – 1)/2}²
? x – 2 = (y – 1)²/4
? (y – 1)² = 4(x – 2)
This represents the equation of a parabola.
Question 13.
The equation of a hyperbola with foci on the x-axis is
(a) x²/a² + y²/b² = 1
(b) x²/a² – y²/b² = 1
(c) x² + y² = (a² + b²)
(d) x² – y² = (a² + b²)
Answer
Answer: (b) x²/a² – y²/b² = 1
Hint:
The equation of a hyperbola with foci on the x-axis is defined as
x²/a² – y²/b² = 1
Question 14.
The equation of parabola with vertex (-2, 1) and focus (-2, 4) is
(a) 10y = x² + 4x + 16
(b) 12y = x² + 4x + 16
(c) 12y = x² + 4x
(d) 12y = x² + 4x + 8
Answer
Answer: (b) 12y = x² + 4x + 16
Hint:
Given, parabola having vertex is (-2, 1) and focus is (-2, 4)
As the vertex and focus share the same abscissa i.e. -2,
parabola axis of symmetry as x = -2
? x + 2 = 0
Hence, the equation of a parabola is of the type
(y – k) = a(x – h)² where (h, k) is vertex
Now, focus = (h, k + 1/4a)
Since, vertex is (-2, 1) and parabola passes through vertex
So, focus = (-2, 1 + 1/4a)
Now, 1 + 1/4a = 4
? 1/4a = 4 -1
? 1/4a = 3
? 4a = 1/3
? a = /1(3 × 4)
? a = 1/12
Now, equation of parabola is
(y – 1) = (1/12) × (x + 2)²
? 12(y – 1) = (x + 2)²
? 12y – 12 = x² + 4x + 4
? 12y = x² + 4x + 4 + 12
? 12y = x² + 4x + 16
This is the required equation of parabola.
Question 15.
If a parabolic reflector is 20 cm in diameter and 5 cm deep then the focus of parabolic reflector is
(a) (0 0)
(b) (0, 5)
(c) (5, 0)
(d) (5, 5)
Answer
Answer: (c) (5, 0)
Hint: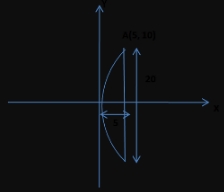
given diameter of the parabola is 20 m.
The equation of parabola is y² = 4ax.
Since this parabola passes through the point A(5,10) then
10² = 4a×5
? 20a = 100
? a = 100/20
? a = 5
So focus of parabola is (a, 0) = (5, 0)
Question 16.
The line lx + my + n = 0 will touches the parabola y² = 4ax if
(a) ln = am²
(b) ln = am
(c) ln = a² m²
(d) ln = a² m
Answer
Answer: (a) ln = am²
Hint:
Given, lx + my + n = 0
? my = -lx – n
? y = (-l/m)x + (-n/m)
This will touches the parabola y² = 4ax if
(-n/m) = a/(-l/m)
? (-n/m) = (-am/l)
? n/m = am/l
? ln = am²
Question 17.
The center of the circle 4x² + 4y² – 8x + 12y – 25 = 0 is?
(a) (2,-3)
(b) (-2,3)
(c) (-4,6)
(d) (4,-6)
Answer
Answer: (a) (2,-3)
Hint:
Given, equation fo the of the circle is 4x² + 4y² – 8x + 12y – 25 = 0
? x² + y² – 8x/4 + 12y/4 – 25/4 = 0
? x² + y² – 2x + 3y – 25/4 = 0
Now, center = {-(-2), -3} = (2, -3)
Question 18.
A rod of length 12 CM moves with its and always touching the co-ordinate Axes. Then the equation of the locus of a point P on the road which is 3 cm from the end in contact with the x-axis is
(a) x²/81 + y²/9 = 1
(b) x²/9 + y²/81 = 1
(c) x²/169 + y²/9 = 1
(d) x²/9 + y²/169 = 1
Answer
Answer: (a) x²/81 + y²/9 = 1
Hint:
Given a rod of length 12 cm moves with its ends always touching the coordinate axes.
Again given a point P on the rod, which is 3 cm from the end in contact with the x-axis.
It is shown in the figure.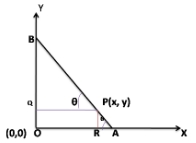
Here AP = 3 cm, AB = 12
Now BP = AB – AP
? BP = 12 – 3
? BP = 9 cm
Again from figure,
?PAO = ?BPO = ? (since PQ || OA and are corresponding angles)
Now in ?BPO,
cos? = QP/BP
? cos? = x/9 …………. 1
Again in ?PAr,
sin? = PR/PA
? sin? = y/3 …….. 2
Now square equation 1 and 2 and then add them, we get
cos² ? + sin² ? = x²/81 + y²/9
? x²/81 + y²/9 = 1 (since cos² ? + sin² ? = 1 )
So, the equation of the locus of a point P is x²/81 + y²/9 = 1
Question 19.
At what point of the parabola x² = 9y is the abscissa three times that of ordinate
(a) (1, 1)
(b) (3, 1)
(c) (-3, 1)
(d) (-3, -3)
Answer
Answer: (b) (3, 1)
Hint:
Given, parabola is x² = 9y
Let P(h, k) is the point on the parabola such that abscissa is 3 times the ordinate.
So, h = 3k ……… 1
Since P(h, k) lies on the parabola
So, h² = 9k ……… 2
From equation 1 and 2, we get
(3k)² = 9k
? 9k² = 9k
? 9k² – 9k = 0
? 9k(k – 1) = 0
? k = 0, 1
When k = 0, h = 0
So k = 1
Now, from equation 1,
h = 3 × 1 = 3
So, the point is (3, 1)
Question 20.
The number of tangents that can be drawn from (1, 2) to x² + y² = 5 is
(a) 0
(b) 1
(c) 2
(d) More than 2
Answer
Answer: (b) 1
Hint:
Given point (1, 2) and equation of circle is x² + y² = 5
Now, x² + y² – 5 = 0
Put (1, 2) in this equation, we get
1² + 2² – 5 = 1 + 4 – 5 = 5 – 5 = 0
So, the point (1, 2) lies on the circle.
Hence, only one tangent can be drawn.













0 Comments:
Post a Comment